Comparison of GFR measurement with [99mTc]-DTPA and clinical methods based on creatinine measurement, in patients over 80 years old

Introduction and aim: The most accurate way of measuring kidney function in GFR. Clinical formulas based on creatinine measurement may be inaccurate mainly in elderly patients (over 80 years of age). In this study we evaluated the accuracy of commonly used clinical formulas by comparing them with a direct measurement with [99mTc]-DTPA ([99mTc]-diethylene-triamine-peracetic acid) in a population of patients aged eighty and older.

Material and methods: 47 patients (27 males and 20 females) with an average age of 81.9 ± 1.7 years, 80% already diagnosed with Chronic Kidney Disease (CKD), were investigated. Two plasma samples were collected between 60-90 and 165-190 minutes after the injection of [99mTc]-DTPA and GFR were calculated. Results: When comparing the GFR values obtained from the various formulae by creatinine levels with the GFR value obtained by measuring [99mTc]-DTPA residue, the following concordance values emerged: (1) MDRD: 55.3%, (2) Cockroft-Gault 55.3% (3) CKD-EPI 57.5% (4) BIS-1 51.1%.

Conclusion: Our data show a poor correlation between all clinical methods and [99mTc]-DTPA, which remains a gold standard for the direct measurement of GFR.

The incidence of Chronic Kidney Disease (CKD) grows with aging and for this reason, it is becoming a public health problem in Western and Eastern Countries [1,2]. In the Literature it has been reported that the proportion of elderly people with CKD represents 53.07% of all elderly patients [3]. Accurate measurement of the glomerular filtration rate (GFR) is a key factor for an early diagnosis, rational staging, and effective management of chronic renal failure.

The formulas for estimating kidney function using serum creatinine are influenced by several variables such as muscle mass, dietary protein intake and systemic diseases [4]. For this reason, algorithms including variables other than creatinine have been widely investigated. Cystatin-C presents some advantages with respect to creatinine for the estimation of GFR, such as serum concentrations independence by muscular mass, absent tubular secretion, complete tubular resorption, and higher sensitivity in identifying initial stages of impaired kidney function. As a result, formulas including cystatin have shown to be superior for determining GFR: for this reason, formulas containing Cystatin-C rather than creatinine have gradually entered clinical use mainly for elderly people [5]. Additionally, equations incorporating serum creatinine and cystatin C tend to be particularly promising when compared with equations that use serum creatinine and Cystatin-C apart [6].

As already demonstrated in two of our previous works [7,8] we found, especially in elderly patients, significant differences using [99mTc]-DTPA compared with clinical methods.

The purpose of the present work was to evaluate the accuracy of the most common clinical formulas, namely the formulas of Cockroft Gault, IDMS-MDRD, CKD-EPI and the more recent Berlin initiative Equation (BIS1) [9] comparing them with the isotopic method that uses [99mTc]-DTPA, in patients with an age greater than or equal to 80 years.

Patients

Our sample included a total of 47 patients, of whom 27 were males and 20 females, with an average age of 81.9 ± 1.7 years. Each patient gave informed consent. The work described was carried out in accordance with The Code of Ethics of the World Medical Association (Declaration of Helsinki). The most recent creatinine values available for each patient were considered, and their levels were determined in our analysis laboratory; the average creatinine values are 1.80 ± 0.80, with a maximum of 3.8 and a minimum of 0.57. With these values, the GFR was calculated using the different formulas available:

(1) MDRD: GFR 38.6 ± 19.6 ml/min;

(2) Cockroft - Gault: 33.7 ± 15.0 ml/min;

(3) CKD-EPI: 38.6 ± 18.5 ml/min;

(4) BIS1: 35.6 ± 13.4 ml/min.

GFR calculation based on the [99mTc]-DTPA method

[99mTc]-DTPA bio-distribution is well represented by a bi-compartment model: the chelate mixes between the vascular and extravascular space and is removed from the plasma by glomerular filtration in the kidneys. This model generates a bi-exponential plasma clearance curve following the initial mixing phase of [99mTc]-DTPA in plasma. It is possible to approximate bi-exponential plasma clearance curves to a mono-exponential plasma clearance curve; assuming that clearance is only by glomerular filtration, the GFR would be described as follows:

$\text{GFR=}\frac{Q}{{{\displaystyle \int }}_0^{\infty }c\left(t\right)dt}$

Where Q is the amount of [99mTc]-DTPA injected and c(t) its plasma concentration [10].

[99mTc]-DTPA (TechneScan®DTPA, Mallinckrodt) was prepared in accordance with the European Pharmacopoeia, Monograph 642 and the quality control of the radiochemical purity, performed by ITLC-SG chromatography, always gave a value >95%. The needle for the infusion set was placed in a peripheral vein. About 180 MBq of [99mTc]-DTPA were injected. Residual activity in the syringe was less than 2% of the dose. Two EDTA blood samples were collected, the first between 60 and 90 minutes and the second between 165 and190 minutes post-injection, using a vein other than the one used for the injection. After centrifugation at 1500 g, duplicate samples of plasma were pipetted, counted in a gamma counter (COBRA auto gamma, Packard) and cross-calibrated weekly with a dose calibrator (PET-DOSE Comecer, Italy).

The GFR was calculated in accordance with the Russell two-sample method [11] and guidelines [12,13] and expressed as ml/min/1.73 MQ. Body surface area was calculated using the DuBois & DuBois formula [14]. The calculated GFR values were always compared with the images and the semi-quantitative data obtained from renal scintigraphy.

Serum creatinine determination and creatinine-based formulae

Serum creatinine (Screat, mg/dl) was measured at the time of the scintigraphic examination using an automatic system, Vitros 5600 (Roche Diagnostic GmbH, Mannheim), by peroxidase-catalyzed oxidation, with a method standardized to IDMS (Isotope Dilution Mass Spectrometry). [99mTc] DTPA GFR values were compared with the GFR values measured using the following Screat-based formulae: CG formula, IDMS-MDRD formula, CKD-EPI formula, Berlin initiative Equation (BIS1) [15] (Table 1).

Statistical analysis

All differences were tested against each other for significance using the t-test (a two-tailed p < 0.05 was considered significant) and the square of Pearson’s correlation coefficient (R2). To compare the four alternative methods used for patient classification, two different statistical tests were performed. The first one simply computed agreement as the percentage of exact agreements observed in the data set. The second one considered the statistical procedure of Bland and Altman [16] and was used to compare the four alternative methods with [99mTc]-DTPA. The limits of agreement between the two different methods were defined as the mean ± 1.96 SD of the difference between the methods.

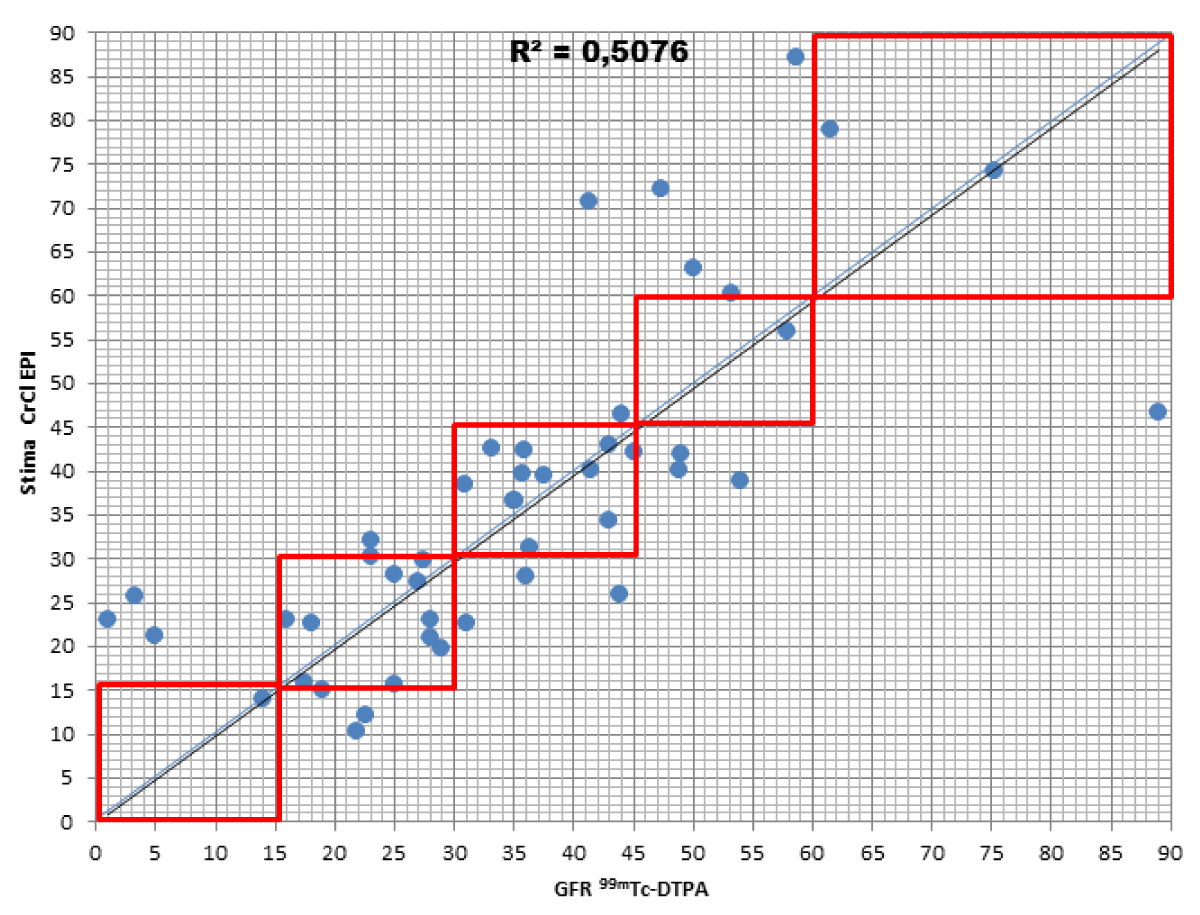
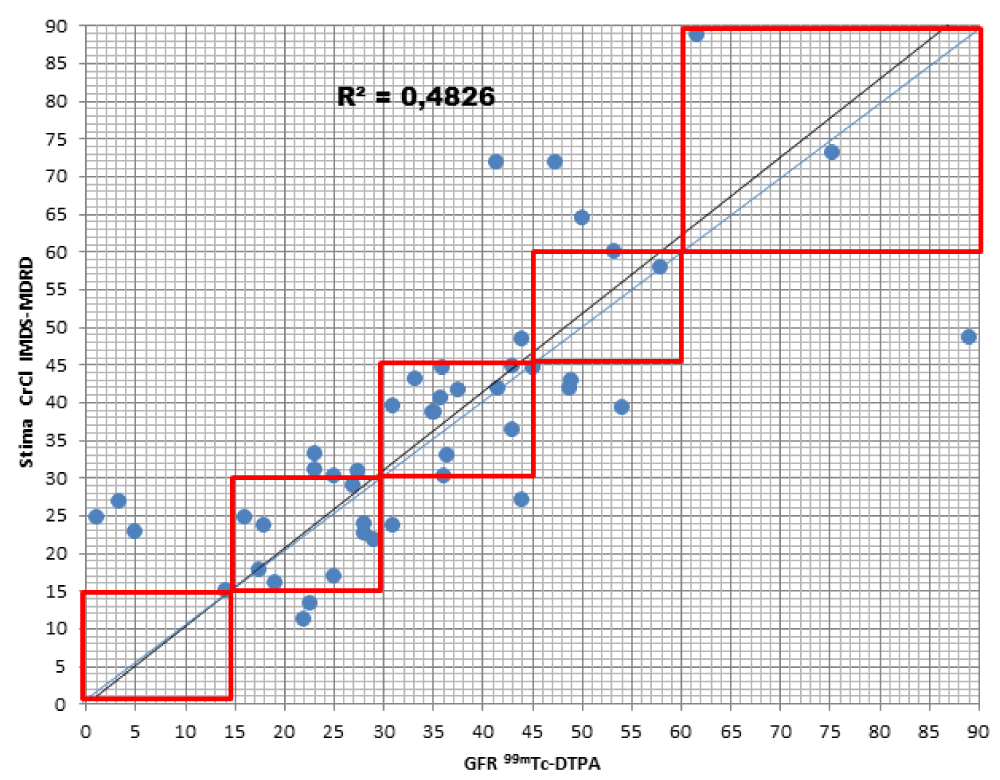
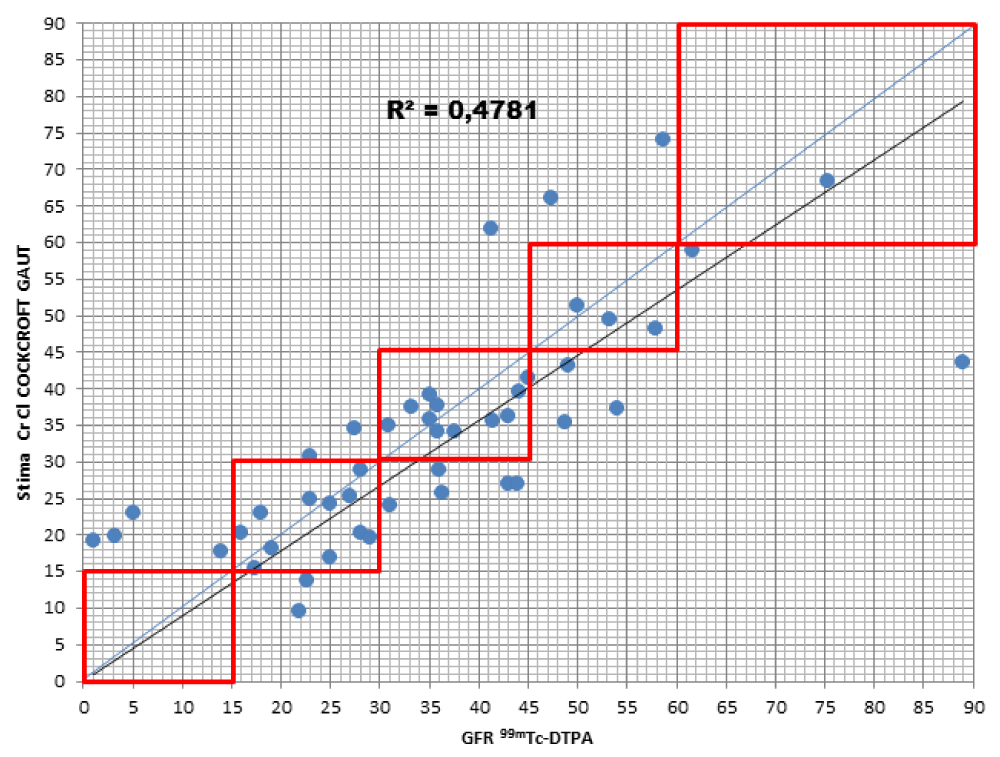
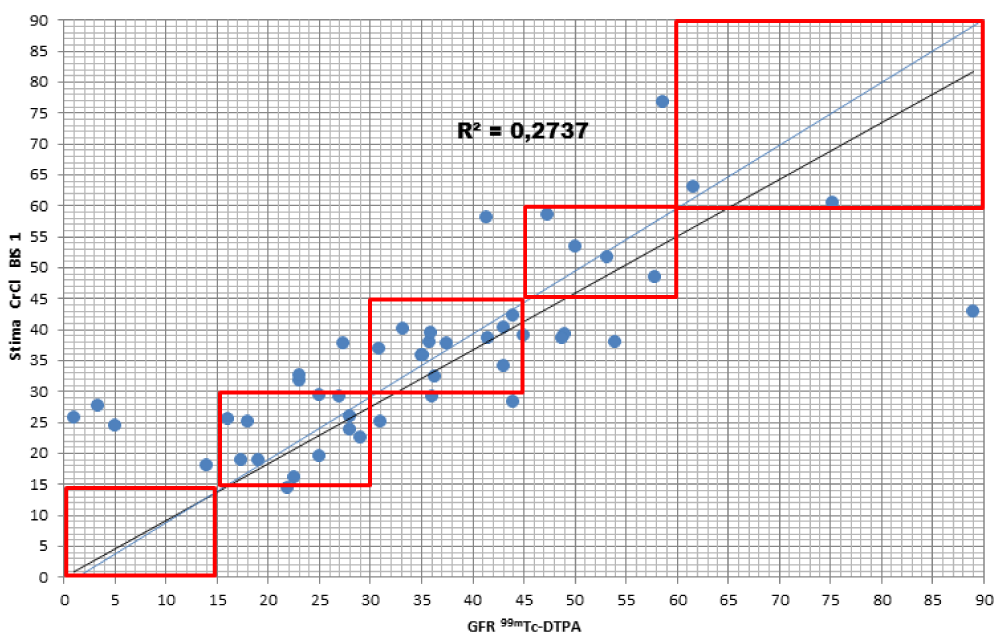
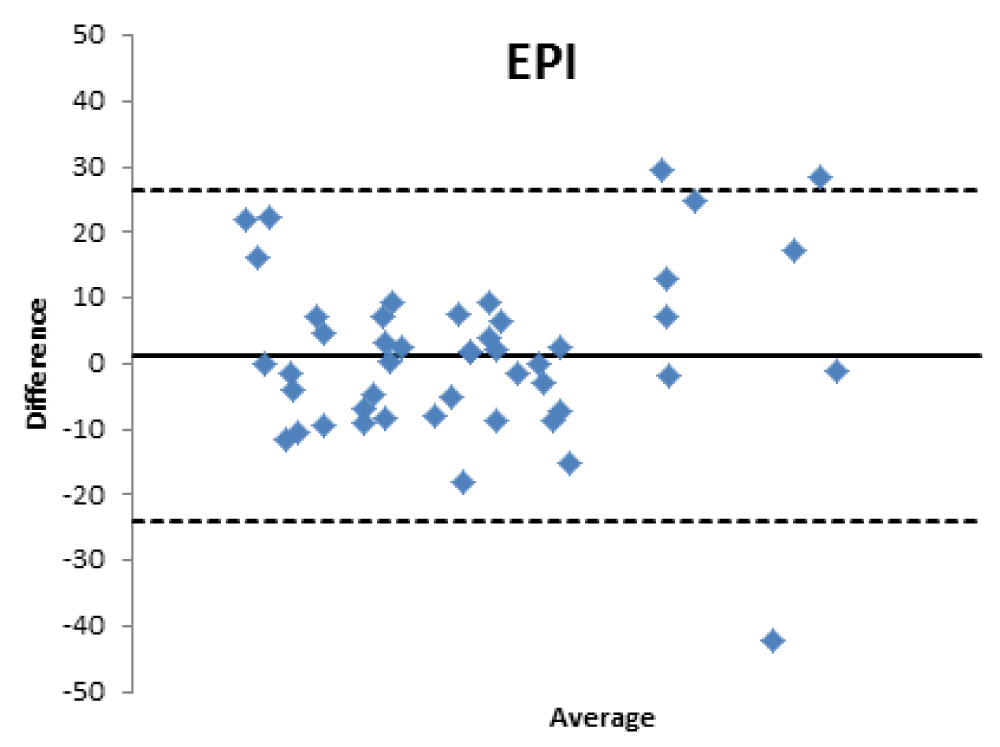
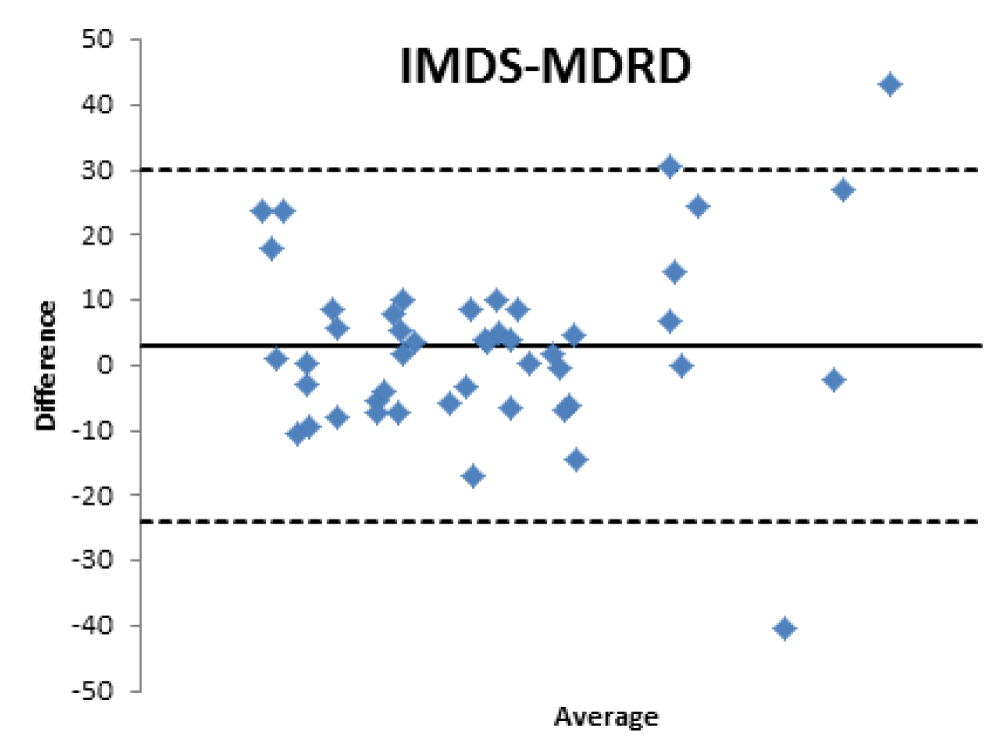
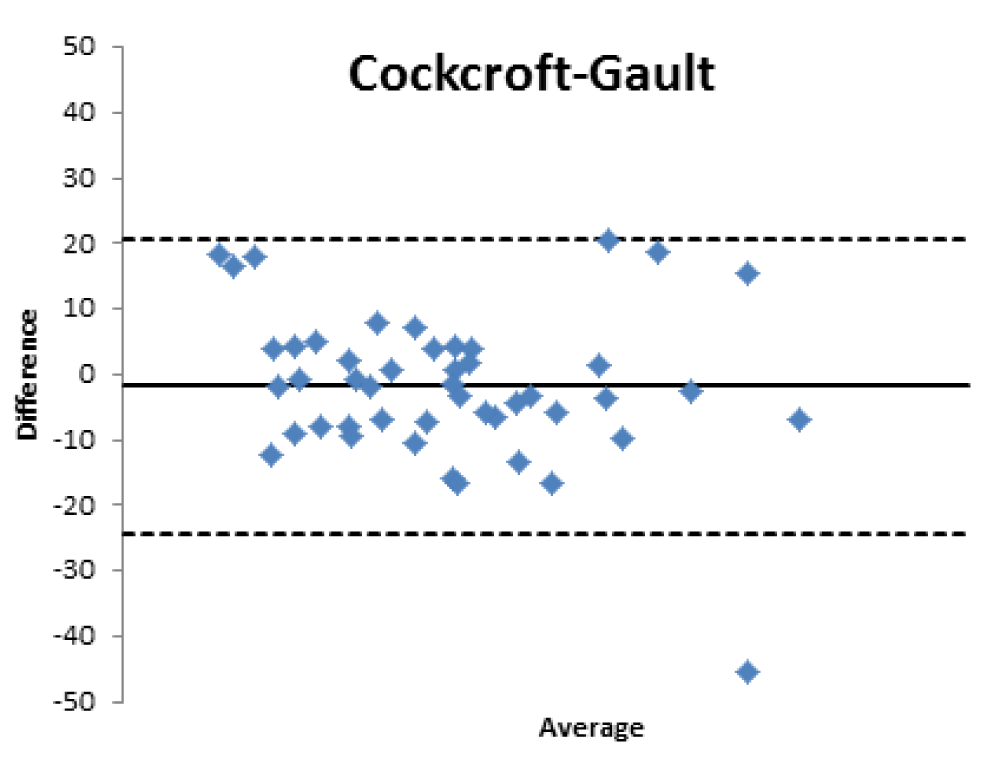
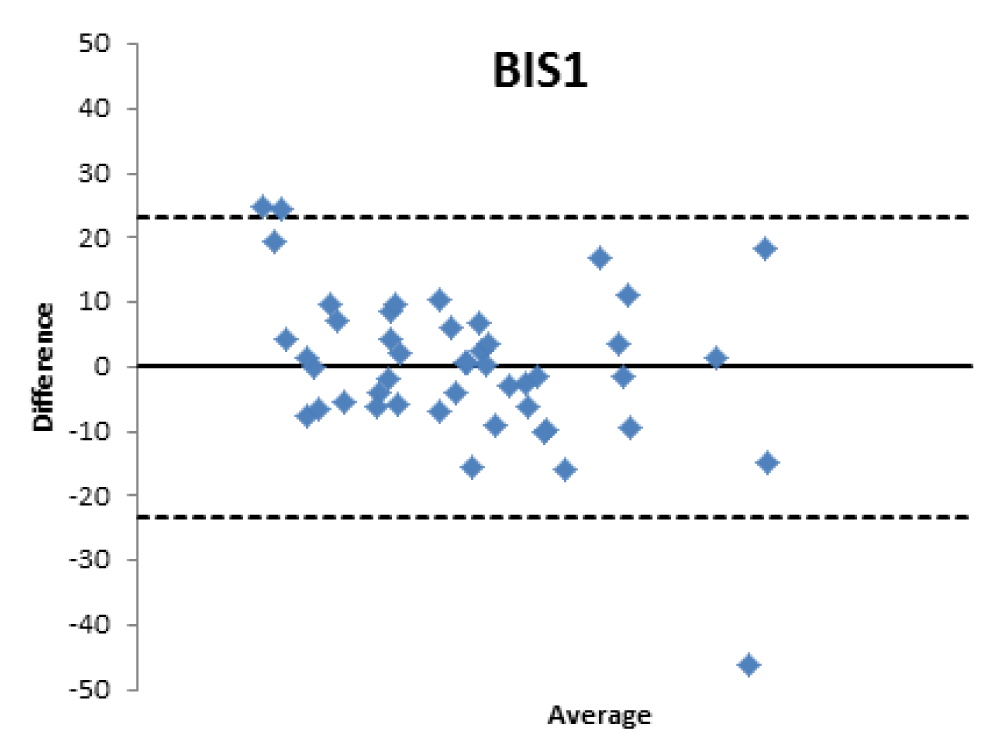
When comparing the GFR values obtained from the various formulae by creatinine levels with the GFR values obtained by measuring [99mTc]-DTPA residue, the following concordance values emerged (Figures 1-4): MDRD: 55.3; Cockroft-Gault: 55.3; CKD-EPI: 57. 5; BIS1: 51.1

The lower percentage of agreement was found between GFR measured with the [99mTc]-DTPA and GFR measured with BIS1; on the contrary, the highest percentage of agreement was found with GFR calculated with the CKD-EPI formula. Cockroft-Gault and MDRD showed to be equivalent, with a level of agreement reaching nearly 55%.

For each formula, the greatest agreement was obtained for GFR values between 45 and 30 ml/min.

Assuming GFR values were measured with [99mTc]-DTPA as a reference, each type of formula was assessed in order to evaluate the differences in allocating patients with respect to classes of Chronic Kidney Disease (CKD) as defined by Lewey AS, et al. [17].

MDRD: the formula returned to a lower level of GFR for 17% of patients compared to the values ​​obtained with [99mTc]-DTPA; in particular, they were all classified in the lowest stage of IRC (V). On the contrary, the formula overestimated GFR in 27.7% of patients, 23.4% of them being classified one stage higher and 4.3% two stages higher of CKD with respect to values measured with [99mTc]-DTPA.

Cockroft-Gault: the formula detected GFR for 25.5% of patients compared to the values ​​obtained with [99mTc]-DTPA; in particular, 23.4% were classified in a lower stage of CKD, 2.1% two stages lower. On the contrary, the formula overestimated GFR in 19.1% of patients, 17% of them being classified one stage higher and 2.1% two stages higher of CKD with respect to the values measured with [99mTc]-DTPA.

CKD-EPI: the formula got a worse GFR for 19.1% of patients compared to the values ​​obtained with [99mTc]-DTPA; in particular, all of them were classified in a lower stage of CKD. On the contrary, the formula overestimated GFR in 23.4% of patients, 21.3% of them being classified one stage higher and 2.1% two stages higher of CKD with respect to values measured with [99mTc]-DTPA.

BIS1: the formula detected a worse GFR for 25.5% of patients compared to the values ​​obtained with [99mTc]-DTPA; in particular, 17% were classified in a lower stage of CKD, 2.1% two stages lower and 6.4% three stages lower. On the contrary, the formula overestimated GFR in 25.5% of patients, 17% of them being classified one stage higher, 6,4% two stages higher, and 2.1 three stages higher of CKD with respect to values measured with [99mTc]-DTPA.

Bland Altman’s analysis is fully represented in Figures 5-8.

For patients aged 80 years old and older, the GFR estimated with formulas used in the clinical setting is moderately reliable, stabilizing at values ​​close to 60% for EPI, CKG and MDRD and lower for BIS1.

For the category of patients taken into consideration, the best agreement was found for the CKD-EPI formula, which is not widely used in the clinical setting, where the use of MDRD and, if anything, of Cockroft-Gault, prevails. However, they have percentage agreement values ​​that are not very different from EPI.

In a recent study, we demonstrated that the level of concordance between [99mTc]-DTPA and clinical formulae was greater in patients younger than 70 years old than in those aged 70 and above (8). In that paper, we showed that MDRD and CKD-EPI equations perform better in younger than older people also if the group of patients aged eighty or older was small. In this paper, we filled this gap by demonstrating that MDRD and EPI perform well also for older patients with a high agreement with the [99mTc]-DTPA measures, with similar levels of accuracy.

Therefore, the differences existing between the formulas that estimate the filtrate and a nuclear medicine measurement method with [99mTc]-DTPA have been confirmed; the [99mTc]-DTPA calculation produces values that are closer to the real values of GFR, as confirmed by Bland Altman’s analysis which shows the superior value of the direct measurement allowed by [99mTc]-DTPA measurement over the estimation of GFR indirectly obtained by clinical formulas. In fact, the standard deviations of the differences are clinically intolerable (s.d.: EPI: 12.89; Cockroft Gault 11.48; MDRD 13.8, BIS1 11.86) and therefore the GFR values calculated with clinical methods are not comparable with those measured with [99mTc]-DTPA. The values obtained from the calculation of the GFR with [99mTc]-DTPA is well correlated with the images and semi-quantitative measurements obtained from the renal scintigraphy unlike the clinical GFR values obtained with the calculation of creatinine. The direct measurement of the GFR can have an important and sometimes decisive impact on the clinical management of the patient, allowing to assume correct therapeutic decisions; for many categories of patients and in certain clinical scenarios it is necessary to correctly know, the highest level of confidence possible, the real value of GFR in order to monitor the effects on the kidney function of drugs such as chemotherapic or new anticoagulant drugs.

Further studies are needed to confirm these results, but certainly, our study highlights the utility of the method which directly calculates the GFR with [99mTc]-DTPA mainly in particular groups of patients. Therefore, we suggest including renal scintigraphy with [99mTc]-DTPA integrated with GFR calculation in order to obtain values as close as possible to the real renal function also in older patients where the probability of the presence of comorbidities is higher.

1. Chen W, Chen W, Wang H, Dong X, Liu Q, Mao H, Tan J, Lin J, Zhou F, Luo N, He H, Johnson RJ, Zhou SF, Yu X. Prevalence and risk factors associated with chronic kidney disease in an adult population from southern China. Nephrol Dial Transplant. 2009 Apr;24(4):1205-12. doi: 10.1093/ndt/gfn604. Epub 2008 Oct 24. PMID: 18952699; PMCID: PMC3203397.
2. Zhang L, Zhang P, Wang F, Zuo L, Zhou Y, Shi Y, Li G, Jiao S, Liu Z, Liang W, Wang H. Prevalence and factors associated with CKD: a population study from Beijing. Am J Kidney Dis. 2008 Mar;51(3):373-84. doi: 10.1053/j.ajkd.2007.11.009. PMID: 18295053.
3. Liu BC, Wu XC, Wang YL, Wang B, Gao J, Zhang QJ, Zhu Y, Zhang XL, Yin LF. Investigation of the prevalence of CKD in 13,383 Chinese hospitalised adult patients. Clin Chim Acta. 2008 Jan;387(1-2):128-32. doi: 10.1016/j.cca.2007.09.020. Erratum in: Clin Chim Acta. 2009 Jul;405(1-2):165. PMID: 18028892.
4. Stevens LA, Coresh J, Greene T, Levey AS. Assessing kidney function--measured and estimated glomerular filtration rate. N Engl J Med. 2006 Jun 8;354(23):2473-83. doi: 10.1056/NEJMra054415. PMID: 16760447.
5. Dharnidharka VR, Kwon C, Stevens G. Serum cystatin C is superior to serum creatinine as a marker of kidney function: a meta-analysis. Am J Kidney Dis. 2002 Aug;40(2):221-6. doi: 10.1053/ajkd.2002.34487. PMID: 12148093.
6. Inker LA, Schmid CH, Tighiouart H, Eckfeldt JH, Feldman HI, Greene T, Kusek JW, Manzi J, Van Lente F, Zhang YL, Coresh J, Levey AS; CKD-EPI Investigators. Estimating glomerular filtration rate from serum creatinine and cystatin C. N Engl J Med. 2012 Jul 5;367(1):20-9. doi: 10.1056/NEJMoa1114248. Erratum in: N Engl J Med. 2012 Aug 16;367(7):681. Erratum in: N Engl J Med. 2012 Nov 22;367(21):2060. PMID: 22762315; PMCID: PMC4398023.
7. Maioli C, Cozzolino M, Gallieni M, Del Sole A, Tagliabue L, Strinchini A, Gaito S, Lecchi M, Cusi D, Lucignani G. Evaluation of renal function in elderly patients: performance of creatinine-based formulae versus the isotopic method using 99mTc-diethylene triamine pentaacetic acid. Nucl Med Commun. 2014 Apr;35(4):416-22. doi: 10.1097/MNM.0000000000000066. PMID: 24457319.
8. Maioli C, Mangano M, Conte F, Del Sole A, Tagliabue L, Alberici F, Galassi A, Cozzolino M. The ideal marker for measuring GFR: what are we looking for? Acta Biomed. 2020 Dec 15;91(4):e2020132. doi: 10.23750/abm.v91i4.9304. PMID: 33525268; PMCID: PMC7927481.
9. Schaeffner ES, Ebert N, Delanaye P, Frei U, Gaedeke J, Jakob O, Kuhlmann MK, Schuchardt M, Tölle M, Ziebig R, van der Giet M, Martus P. Two novel equations to estimate kidney function in persons aged 70 years or older. Ann Intern Med. 2012 Oct 2;157(7):471-81. doi: 10.7326/0003-4819-157-7-201210020-00003. PMID: 23027318.
10. Fleming JS, Wilkinson J, Oliver RM, Ackery DM, Blake GM, Waller DG. Comparison of radionuclide estimation of glomerular filtration rate using technetium 99m diethylenetriaminepentaacetic acid and chromium 51 ethylenediaminetetraacetic acid. Eur J Nucl Med. 1991;18(6):391-5. doi: 10.1007/BF02258429. PMID: 1908780.
11. Russell CD, Bischoff PG, Kontzen FN, Rowell KL, Yester MV, Lloyd LK, Tauxe WN, Dubovsky EV. Measurement of glomerular filtration rate: single injection plasma clearance method without urine collection. J Nucl Med. 1985 Nov;26(11):1243-7. PMID: 3903074.
12. Blaufox MD, Aurell M, Bubeck B, Fommei E, Piepsz A, Russell C, Taylor A, Thomsen HS, Volterrani D. Report of the Radionuclides in Nephrourology Committee on renal clearance. J Nucl Med. 1996 Nov;37(11):1883-90. PMID: 8917197.
13. Fleming JS, Zivanovic MA, Blake GM, Burniston M, Cosgriff PS; British Nuclear Medicine Society. Guidelines for the measurement of glomerular filtration rate using plasma sampling. Nucl Med Commun. 2004 Aug;25(8):759-69. doi: 10.1097/01.mnm.0000136715.71820.4a. PMID: 15266169.
14. DuBois D, DuBois EF. A formula to estimate the approximate surface area if height and weight are known.  Ann Intern Med 1916;17:863-871
15. Fliser D, Ritz E. Serum cystatin C concentration as a marker of renal dysfunction in the elderly. Am J Kidney Dis. 2001 Jan;37(1):79-83. doi: 10.1053/ajkd.2001.20628. PMID: 11136171.
16. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986 Feb 8;1(8476):307-10. PMID: 2868172.
17. Levey AS, Eckardt KU, Tsukamoto Y, Levin A, Coresh J, Rossert J, De Zeeuw D, Hostetter TH, Lameire N, Eknoyan G. Definition and classification of chronic kidney disease: a position statement from Kidney Disease: Improving Global Outcomes (KDIGO). Kidney Int. 2005 Jun;67(6):2089-100. doi: 10.1111/j.1523-1755.2005.00365.x. PMID: 15882252.